|
A
McCready használata
Néhány
gondolattal kiegészíteném
Bzernai János: "PDA"
és "Rohanjak
vagy ne rohanjak"
dokumentumokban leírtakat:
(a felhasznált irodalom és ábrák a TELJESÍTMÉNYREPÜLÉS c.
kiadványból vannak, Szereday Pál írásából)
Tartalomjegyzék:
Sebesség
poláris
Egyszerűsített sebesség poláris
Távrepülés szakaszai
A legelőnyösebb
siklósebesség megválasztása
Egy gyakorlati példa
A
McCready tárcsa
McCready tárcsa szerkesztése
McCready használata a
játékban
A
McCready tárcsának, vagy sikló computernek az a célja, hogy a
termikek közötti sikló sebességet úgy tudjuk megválasztani, hogy
a siklásban, és a következő termikben emelkedéssel eltöltött idő
összesen a lehető legrövidebb legyen, vagyis a legnagyobb
átlagsebességgel tudjunk repülni.
Induljunk az alapoktól, tanulmányozzuk egy kicsit
a repülőgépek sebesség polárisát:
Mint tudjuk, a vitorlázó
repülőgépek sikló sebessége az állásszögtől, vagyis a repülőgép
földhöz viszonyított hajlásszögétől ("γ"siklószög)
függ. Ha meghatározzuk a különböző siklószögekhez tartozó
siklási és merülési sebességeket, és ezt egy derékszögű
koordináta rendszerben azonos léptékben ábrázoljuk, akkor
megkapjuk a repülőgép sebesség polárisát:

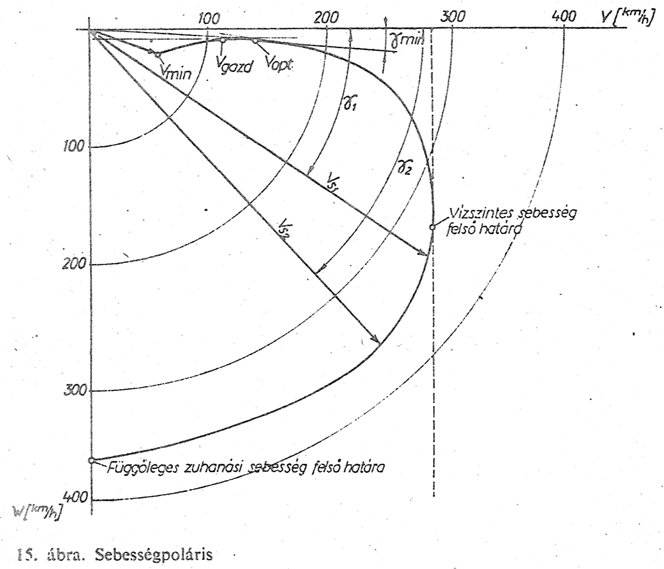
A
vízszintes tengelyre a "v" vízszintes sebességeket, a függőleges
tengelyre a "w" merülő sebességeket rajzoljuk föl. Az értékek
összekötése után kapjuk a görbét. Egyes pontjaihoz az origóból
húzott vonalak megadják a repülőgép siklási vektorait, ebből
következik, hogy ez a vonal és a vízszintes tengely között
bezárt szög a siklószög, amennyiben a "v" és "w" tengelyeket
azonos léptékben vesszük föl! A Condorban grafikonján ez
nem így van, így a siklószögek hamisak! De erről kicsit
később.
A
sebességi polárisról a következő főbb jellemzők olvashatók le:
| "γ" min
(ill. "ε" max.): |
A repülőgép
legkisebb siklószöge (ill. a legnagyobb siklószáma), az
origóból húzott érintő. |
| vs opt |
optimális
sebesség, vagyis a legjobb siklószámhoz tartozó sebesség
. |
| vs
gazd |
gazdaságos
sebesség, vagyis a legkisebb merülő sebességhez tartozó
sebesség. |
| wmin |
a legkisebb
merülő sebesség, a polárishoz húzott vízszintes érintő. |
| vs min |
a legkisebb
sikló sebesség, a görbe legelső pontjához húzott
függőleges érintő. |
| vmax |
siklásban
elérhető legnagyobb vízszintes sebesség, polárishoz jobb
oldalánál függőleges érintő. |
| vs max |
elméletileg
elérhető legnagyobb zuhanó sebesség. |
Egyszerűsített
sebesség poláris.
A vitorlázórepülésben gyakorlatban alkalmazott sebesség poláris
az előbb leírtnak egy egyszerűsített változata. Vízszintes
tengelyen a vmax
kb 70%-ig rajzoljuk meg a grafikont, a függőleges tengelyt m/s
szerint skálázzuk. Mivel a görbe az eltérő skálázás miatt
torzul, siklószöget közvetlenül nem mérhetünk belőle. A gyakori
számolgatások elkerülése végett állt. a siklószám görbét is
berajzolják, ekkor a függőleges tengelyre kettős skálázás kerül:

A
Condorban is egyszerűsített sebesség polárist lehet a gépekről
találni, siklószám görbe nélkül:
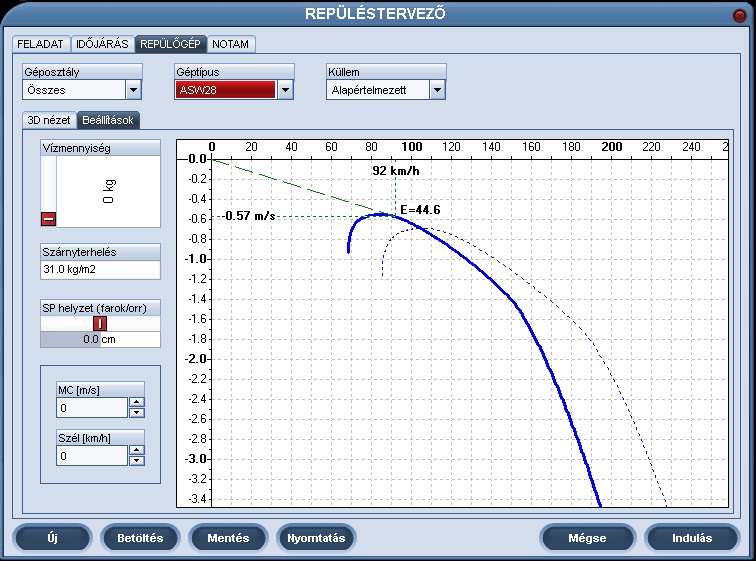
A
leolvasható értékek ugyanazok, leolvasásuk ugyanúgy történik,
mint a teljes sebesség polárison.
Vizsgáljuk meg, hogy a
távrepülések milyen szakaszokból épülnek föl:
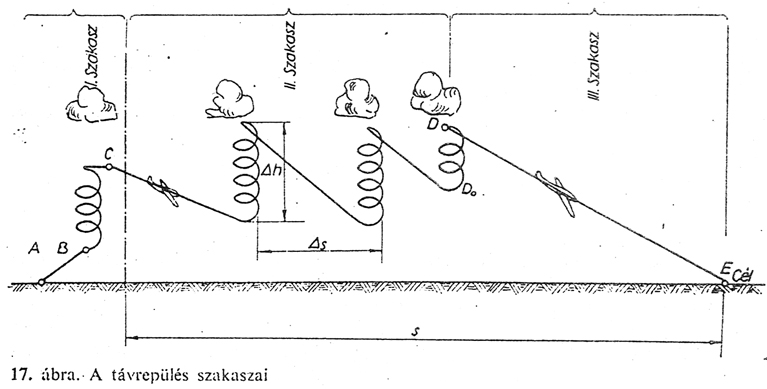
I.
szakasz: Emlkedés. Ez elvileg nem kellene, hogy számítson, de
igyekezzünk minél előbb felszállni, és kitapasztalni az
időjárást, az emeléseket.
II. szakasz: Magasságnyerések és siklások szakasza. Ez a
legdöntőbb. Ha a siklási vagy emelkedési szakaszok részidejét
tudjuk csökkenteni, akkor máris javul az átlagsebességünk.
III. szakasz: besiklás. A sebesség értékelésű céltávoknál van
jelentősége, törekedni kell a biztonságra, hogy normálisan
hazaérjünk.
A legelőnyösebb
siklósebesség kiszámolása (McCready computer nélkül):
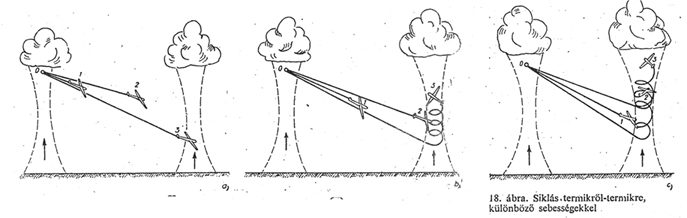
Vegyünk
egy példát. Adott három azonos repülőgép, mindegyik a "0"
pontról indul, azonos pillanatban. Az 1. gép a legkisebb
merüléshez tartozó sebességgel megy, a 2. gép a gazdaságos
sebességgel megy, a 3. gép mindkettőnél kicsit gyorsabban. A 3.
gép nagyobb siklószöge miatt alacsonyan ért ugyan a termikhez,
de annak felhajtóerejét kihasználva a többiek előtt hagyhatta el
azt. De vajon mi az a sebesség, ahol már a sietség káros, és az
elvesztett magasságot nem tudja visszaszerezni annyi idő alatt,
míg a többiek beérik?
Célunk
tehát kideríteni, mely sikló sebességgel érjük el a legnagyobb
átlagsebességet, ami a siklási és az emelkedési szakaszból
tevődik össze!
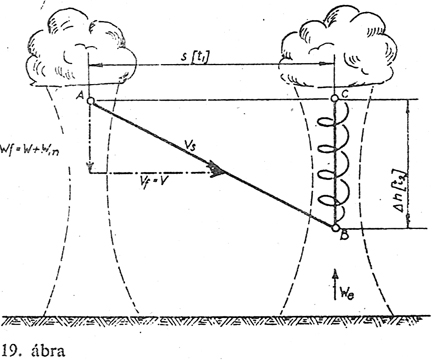
A
repülőgépünk "A" pontból siklik "B" pontba, "vs"sebességgel,
miközben "wf" sebességgel merül. Jó közelítéssel "vs"
sebességet a vízszintes összetevőjével, "v" sebességgel
azonosnak tekintjük. (A két termik közötti "wm"
leáramlás hozzáadódik a gép merülő sebességéhez, a variométer
ezért mutat "w"+"wm"="wf" értéket). A gép
a következő termiket "B" pontban éri el, innen emelkedik "we"
függőleges sebességgel a "C" pontig. A "B" és "C" pontok között
"Δh" magasságot nyer "t2" idő alatt.
az
algebrai számítás levezetésétől eltekintenék, ha valakit
érdekel, szívesen beszkennelem a könyvből. A példánkhoz elég
annyi, hogy a levezetés végére a következő képlet (5)
jött ki:
Az
egyenlet geometriai levezetését viszont bemásolom:
A levezetés alapját az a szabály képezi, mely szerint hasonló
háromszögek megfelelő oldalainak méretei között egyenes
arányosság áll fenn:
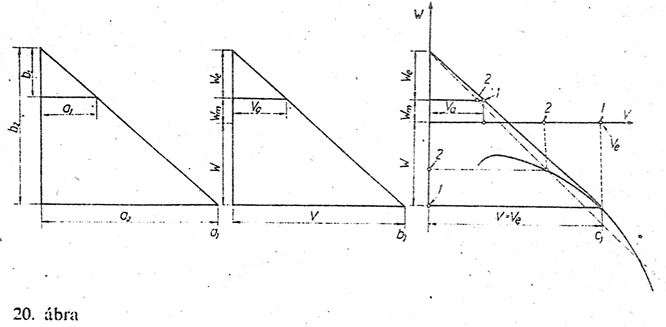
A 20/a
ábrán látható egymásba rajzolt két háromszög hasonló, mert
szögeik egyenlők. Az ismert szabály alapján felírható a
következő arányosság:
A 20/b
ábrán az (5) képletben szereplő mennyiségeket
ábrázoltuk oly módon, hogy az előbbi aránypárt felírva ezt a
képletet kapjuk meg.
A 20/c
ábrán látható, hogy ugyanez valamelyik vitorlázógép sebesség
polárisán is tökéletesen alkalmazható. Az így ábrázolt
hasonló háromszögek egyes oldalai sebességmennyiségeket
jelentenek, mégpedig a koordináta tengelyek léptékének
megfelelően.
Ha a polárisba berajzolt összefüggéseket vizsgáljuk,
megállapítható, hogy a "we" és "wm"
értékek adottak, mert meteorológiai tényezők szabják meg őket. a
"v" és a hozzá tartozó "w" értéke viszont változó lehet, így
nekünk kell kiválasztani, mely az a sebesség, amivel a
legnagyobb átlagsebesség érhető el.
Akár
próbálgatással, akár ránézésre megállapíthatjuk, hogy az
átlagsebesség akkor a legnagyobb, ha az előbbiek szerint
berajzol háromszögek közös átfogóinak egyenese a görbét érinti.
Ezt a
következő módon szerkeszthetjük meg:
A vitorlázó sebesség polárisának függőleges tengelyére, az
origóból kiindulva először felmérjük a levegő "wm"
merülő sebességét, majd ennek a végpontjából a "we"
emelkedési sebességet, amivel várhatóan a következő termikben
emelkedni fogunk. Ennek felső pontjából érintőt húzunk a
polárishoz. Az így kapott sebesség az elérhető legnagyobb
átlagsebességhez tartozó sebesség ("we").
Ez az
a sebesség, amit az MC megfelelő értékre állításával a
sikló-computerünk a Condorban jelezni fog.
Egy
gyakorlati példán megpróbálom bebizonyítani, hogy a McCready
alkalmazása tényleg nagy előnyökkel jár. Adott két termik, 10
km-es távolságban, 4 m/s-os emeléssel. Szél nincs. A gépek 1500
m-ről indulnak, és a következő termikben odáig emelkednek. Nos,
nézzük mennyi ideig tart mindez: (A Condor repülőgép adatokból
olvastam ki a poláris alapján, példának az ASW-28
repülőgépet vettem).
|
|
sebesség |
merülés |
siklásban eltöltött idő |
siklásban magasság vesztés, ennyit kell visszaemelkedni |
emelkedéshez szükséges idő (sec) |
Összesen (sec) |
|
A |
130 km/h |
-1,10 |
276,9 sec |
304,6 m |
76,2 sec |
353,1 |
|
B |
160 km/h |
-1,71 |
225,0 sec |
384,8 m |
96,2 sec |
321,2 |
|
C |
190 km/h |
-3,20 |
189,5 sec |
606,3 m |
151,6 sec |
341,1 |
Mint a
példából látható, a "B" jelű gép tud a következő
termikből legelsőnek tovább indulni. Amikor a "C" jelű gép 20
másodperc múlva követi, a "B"-nek már kb. 800 m előnye lesz. Az
"A" jelű repülőgépről nem is beszélve, 32 másodperc alatt a "B"
kb 1400 m tesz meg. Mindezt egy 10km-es szakaszon, egy
termikeléssel, csak a sikló sebesség helyes megválasztásával
nyerte!
Ha ezek után a grafikonon ellenőrizzük, a 4.0 MC
állásnál az ASW-28 ideális sikló sebessége: 158 km/h, tehát
ezt tartva tudunk a legjobb átlagsebességgel repülni.
McCready tárcsa:
A
legjobb átlagsebességet adó siklósebességek egyszerű és
áttekinthető meghatározását biztosítja - termikről termikre való
siklás közben - a McCready féle tárcsa. Előnye, hogy kezelése
nem igényel nehéz számításokat, viszont nagy pontossággal veszi
figyelembe a siklás közben szüntelenül változó merülő és emelő
zónák sebességmódosító hatásait.

Ez a
tárcsa lényegében egy sebességskálával ellátott forgatható
gyűrű, melyet a veriométer skálája köré helyeznek. Siklás közben
a variométer tűje állandóan mutatja a repülőgép "wf"
merülő sebességét, így a tárcsán különböző sebességeket jelöl
meg. A pilóta feladata mindössze annyi, hogy a tárcsa
kezdőpontját rá kell állítania az emelkedés skála azon értékére,
ami a következő termik várható emelésével megegyezik. Ezt
követően olyan sebességen kell tartania a gépet, amit a
variométer tűje a tárcsán megjelöl.
A
gyakorlatban ez egy kicsit bonyolultabb feladat. Tételezzük fel,
hogy 80km/h sebességgel utazva a variométer tűje a tárcsán pont
erre mutat. Ebben az esetben tehát helye sebességgel siklunk. Ha
azonban átutazunk egy merülő zónán, a variométer a nagyobb
merülés miatt a 85 km/h-ra fog mutatni. A pilóta ekkor a
sebességét megnöveli erre az értékre, ám ez miatt a variométer
tűje tovább süllyed, még nagyobb sebességet jelölve meg.
Helyesen megszerkesztett tárcsánál azonban ez a jelenség csak
addig ismétlődik, míg a variométer által kijelölt sebességet
utoléri a sikló sebesség, vagyis elértük a legnagyobb
átlagsebességhez tartozó tényleges sikló sebességet.
McCready tárcsa
szerkesztése.
Ha
meghatározzuk, hogy a helyes sebességekhez milyen variométer
állások tartoznak, és az összetartozó értékeket folyamatos
görbével ábrázoljuk, megkapjuk a McCready tárcsa szerkesztéséhez
szükséges görbét (42. ábra)

[42. ábra - zoom]
Példa: A
42. ábrán példaképpen meghatározzuk a "Super Futár" We=2
m/s várható termikerősséghez tartozó McCready görbéjét.
A 21. ábrán ábrán látható a Műszaki Egyetem által mért Super
Futár polárisa. A szerkesztéshez a statisztikai mérések alapján
megállapított merülő-zónák méretét vesszük alapul, ami 20%
(wm=0,2 ˇ we).
Ezután a a ve siklósebességeket és va
átlagsebességeket berajzoljuk a különböző emelkedési
sebességekhez ( pl. 0-6 m/s -ig). Az ábrán csak az 1 m/s-os van
berajzolva.

[21. ábra - zoom]
A
pontokat összekötve megkapjuk a görbéket, amik már a rész
sebességekkel való számolásokhoz is segítséget adnak.
Gyakorlati repülés, MC beállítása:
A
játékban, ahol már PDA, sikló computer és elektromos variométer
segít minket, sokkal egyszerűbb dolgunk van.
A feladat indulása előtti emelkedési szakaszt felhasználjuk az
átlagemelések kitapasztalására, majd ezt az értéket a computerbe
beállítjuk (A képeken a Jantar 2B-nél MC: 2,5 állítottam be,
vagyis 2,5 m/s átlagemelésekre számítok). Ehhez tartozó sikló
sebességet az elektromos variométer két módon jelzi:
Az első
képen az elektromos variométer "vario" állásban van, a piros
háromszög (és a csipogás) az emelkedést/süllyedést jelzi
(pontosan azt, amit a variométer).
A kijelzőn szereplő értékek a következők:
Felül: magasságot mutatja, pontosan azt, amit a
magasságmérő is mutat.
Középen, balról: üzemmód (V - vario), utána az átlag
emelés vagy merülés (ugyanaz, mint a PDA 4. oldalán látható, a
képen épp -1.1), valamint jobboldalt az MC értéknek megfelelő
sebesség tartásához segítség. Ez az ikon jelzi, hogy lassítani
(nyilak fölfelé) vagy gyorsítanunk (nyilak lefelé) kell. Ha csak
egy vonal látszik, a sebesség megfelelő.
Alul: a beállított MC érték látható.
Ha az
elektromos variot átváltjuk siklás üzemmódba (2. kép), a
kijelzőn megjelenő értékek nem változnak, csak az üzemmód vált
S-re. A piros háromszög és a csipogás jelentése viszont
változik: ha a piros háromszög negatív értéket mutat, akkor
gyorsítanunk, ha pozitív értéket, akkor lassítanunk kell. Ha
0-án áll, akkor az MC szerinti sebességen repülünk.
A sikló
computer figyelembe veszi a merülő és emelkedési zónákat is, és
folyamatosan változtatja a szükséges sebességet, mindig a
legoptimálisabbat beállítva.

1. kép: Elektromos
variométer vario üzemmódban

1. kép: Elektromos
variométer siklás üzemmódban
|